Generalised geometric Langlands
Generalisations of geometric Langlands from twisted S-duality
This project is joint with Surya Raghavendran.
The geometric Langlands conjecture, originally formulated by Laumon, Beilinson and Drinfeld (Drinfeld, 1983; Laumon, 1987; Beilinson & Drinfeld, 1996; Beilinson & Drinfeld, 1991) and sharpened by Arinkin and Gaitsgory (Arinkin & Gaitsgory, 2015), is roughly the statement that the category of \(\mathcal{O}\)-modules on the moduli space of \(^LG\) local systems on a curve \(C\) is equivalent to the category of \(\mathcal{D}\)-modules on the moduli space of \(G\)-bundles on \(C\). Here, \(\mathcal{O}\) is the sheaf of functions, \(\mathcal{D}\) is the sheaf of differential operators, and \(G\) and \(^LG\) are Langlands dual groups (Springer, 1998).
In their famous paper (Kapustin & Witten, 2007), Kapustin and Witten realised that this conjectural mathematical equivalence, together with the closely related geometric Satake theorem (Mirković & Vilonen, 2007), could be explained physically in terms of “S-duality” of \(\mathcal{N}=4\) 4d supersymmetric Yang-Mills theory (SYM), a non-perturbative duality relating a \(G\)-gauge theory at strong coupling to an \(^LG\)-gauge theory at weak coupling.
\(S\)-duality arises from a symmetry of type IIB string theory. In (Raghavendran & Yoo, 2019), \(S\)-duality was written explicitly in a supersymmetric sector of type IIB string theory, which can be described as a topological string. In particular, the authors described a “twisted S-duality” map on the closed topological string fields which can couple to a stack of D3 branes. Applying this twisted S-duality map to a particular closed string field yields the usual geometric Langlands conjecture. However there are many other closed string fields to couple to, leading to many variations of the geometric Langlands duality to explore.
This project contains within it a number of individually interesting sub-projects:
Hamiltonian deformations of the stack of Higgs bundles
The closed-string fields we study induce novel deformations of the category of sheaves on the moduli of Higgs vector bundles \(\mathcal{H}\mspace{-1 mu}\mathit{iggs}\). These deformations are expected to be exchanged by the duality. The first step for us in understanding and computing these deformations comes from recognizing that they arise from a Hamiltonian deformation of the shifted cotangent bundle to the moduli of Higgs bundles. In particular, there is a map from closed topological string fields on spacetime (i.e. cyclic cohomology) to functions on the shifted cotangent bundle to \(\mathcal{H}\mspace{-1 mu}\mathit{iggs}\) (i.e. polyvector fields on \(\mathcal{H}\mspace{-1 mu}\mathit{iggs}\)).
We are currently working on computing this map explicitly, in terms of an integral transform whose integral kernel is the Chern character of a certain universal bundle.
Compatibility between S-duality and T-duality
One consequence of S-duality, the Dolbeault geometric Langlands conjecture, states that after compactifying 4d \(\mathcal{N}=4\) Yang-Mills on a Riemann surface \(C\), the S-duality transformation in 4d becomes T-duality relating the moduli spaces of \(G\) and \(^LG\) Higgs bundles (Bershadsky et al., 1995; Harvey et al., 1995; Kapustin & Witten, 2007). Mathematically, this is the prediction that
\[\text{QCoh}(\mathcal{H}\mspace{-1 mu}\mathit{iggs}_G(C))\simeq\text{QCoh}(\mathcal{H}\mspace{-1 mu}\mathit{iggs}_{^LG}(C)),\]which has been borne out in various levels of generality for dense open subsets of each side, but most prominently by Hausel and Thaddeus in type A and Donagi and Pantev for arbitrary reductive groups (Hausel & Thaddeus, 2003; Donagi & Pantev, 2012; Arinkin, 2013; Arinkin & Fedorov, 2016; Derryberry, 2020).
In all cases, this equivalence is implemented by a Fourier-Mukai transform with kernel a Poincaré line bundle. We conjecture and hope to prove that the map from closed string fields to polyvector fields on \(\mathcal{H}\mspace{-1 mu}\mathit{iggs}\) mentioned above is equivariant with respect to the actions of S- and T-duality, i.e. that the following diagram is commutative:
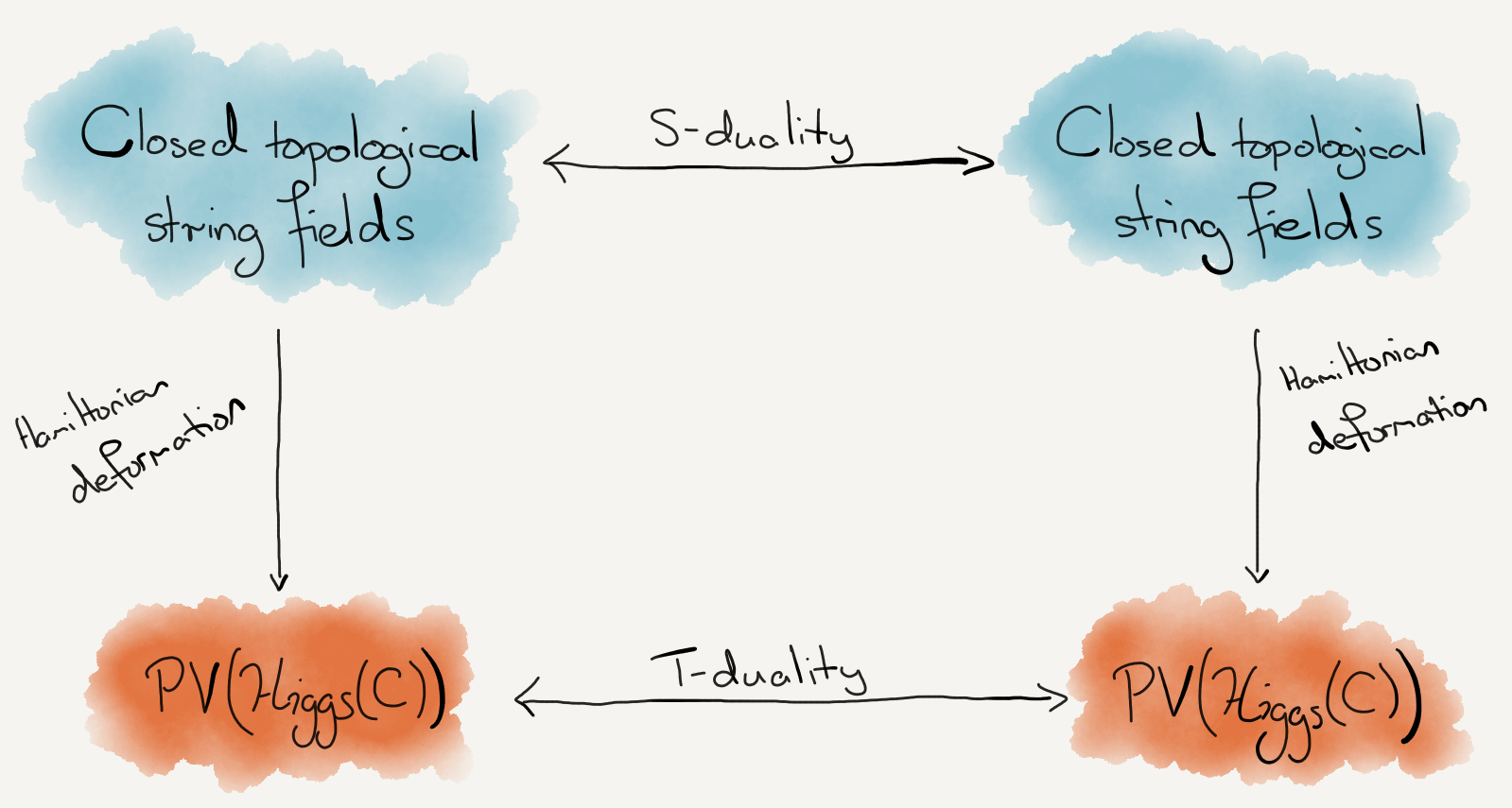
Deformations of the categories of branes
The novel equivalences between categories of branes we wish to understand all arise as deformations of the equivalence proposed in the Dolbeault geometric Langlands conjecture. The way this equivalence, and consequently its deformations, arises in this setting is somewhat subtle. Namely, S-duality acts on the data of a higher geometric quantisation of the shifted cotangent bundle to \(\mathcal{H}\mspace{-1 mu}\mathit{iggs}\).
This yields complications: until extremely recently higher geometric quantisation of shifted symplectic stacks was not a well understood topic, and was only defined for (shifted) cotangent bundles. This has now changed, with Safronov’s recent preprint on shifted geometric quantizations (Safronov, 2020). The deformation theory of shifted geometric quantizations, and how deformations interact with automorphisms, is still an open question however.
Our investigations will shed light on what such a deformation theory would be comprised of. To this end, we are investigating a particular \(\mathbb{N}\)-indexed family of pairs of closed string fields related by S-duality, generalising the geometric Langlands conjecture (which is the case \(n=0\)). In the \(n=1\) case we can conjecture that the category of modules for the Clifford algebra \(\text{Cl}_1\) in vector bundles on \(C\) is equivalent to a yet to be identified subcategory of modules for the Rees algebra of differential operators on \(\mathcal{H}\mspace{-1 mu}\mathit{iggs}\). It is our hope that the work of Safronov may give us the tools required to specify the precise subcategory in question.
References:
- Two-dimensional l-adic representations of the fundamental group of a curve over a finite field and automorphic forms on \rm GL(2)American Journal of Mathematics, 1983
- Correspondance de Langlands géométrique pour les corps de fonctionsDuke Mathematical Journal, 1987
- Quantization of Hitchin’s fibration and Langlands’ programIn Algebraic and geometric methods in mathematical physics (Kaciveli, 1993), 1996
- Quantization of Hitchin’s integrable system and Hecke eigensheaves1991
- Singular support of coherent sheaves and the geometric Langlands conjectureSelecta Mathematica. New Series, 2015
- Linear algebraic groups1998
- Electric-magnetic duality and the geometric Langlands programCommunications in Number Theory and Physics, 2007
- Geometric Langlands duality and representations of algebraic groups over commutative ringsAnnals of Mathematics. Second Series, 2007
- Twisted S-DualityPreprint, arXiv: 1910.13653, 2019
- Topological reduction of 4D SYM to 2D σ-modelsNuclear Physics. B. Theoretical, Phenomenological, and Experimental High Energy Physics. Quantum Field Theory and Statistical Systems, 1995
- Reducing S duality to T dualityPhysical Review. D. Third Series, 1995
- Mirror symmetry, Langlands duality, and the Hitchin systemInventiones Mathematicae, 2003
- Langlands duality for Hitchin systemsInventiones Mathematicae, 2012
- Autoduality of compactified Jacobians for curves with plane singularitiesJournal of Algebraic Geometry, 2013
- Partial Fourier-Mukai transform for integrable systems with applications to Hitchin fibrationDuke Mathematical Journal, 2016
- Stacky dualities for the moduli of Higgs bundlesAdvances in Mathematics, 2020
- Shifted geometric quantizationPreprint, arXiv: 2011.05730, 2020