Self-dual geometric Langlands
A self-dual generalisation of geometric Langlands from Theory X
The mathematical study of the linearisation of symmetries, representation theory, has in modern times evinced deep ties to the physics of quantum field theories (QFTs). These ties are exemplified by the 2007 work of Anton Kapustin and Ed Witten on \(\mathcal{N}=4\) 4d super Yang-Mills theory (SYM), a far reaching generalisation of electromagnetism. Kapustin and Witten realised that the geometric Langlands program – the holy grail of modern geometric representation theory – could be understood as the symmetry of SYM given by exchanging the electric and magnetic fields (Kapustin & Witten, 2007).
The goal of this project is to formulate and prove a self-dual version of the geometric Langlands program. The existence of self-dual Langlands is predicted by the symmetries of the QFTs of class \(\mathcal{S}\) of Gaiotto, Moore and Neitzke (Gaiotto et al., 2013), which are themselves derived from a mysterious six-dimensional ur-theory known as “Theory \(\mathfrak{X}\)”. Since its discovery, Theory \(\mathfrak{X}\) has contributed widely both to mathematics (e.g. in knot theory (Witten, 2012)) and to physics (e.g. the influential AGT correspondence (Alday et al., 2010)).
A schematic overview of the derivation of usual and self-dual Langlands is presented in the diagram below. Roughly, higher dimensional theories give rise to lower dimensional theories through a process called “compactification” (the black arrows) and relative theories (Freed & Teleman, 2014) give rise to absolute theories through a process called “absolution” (the blue arrows).
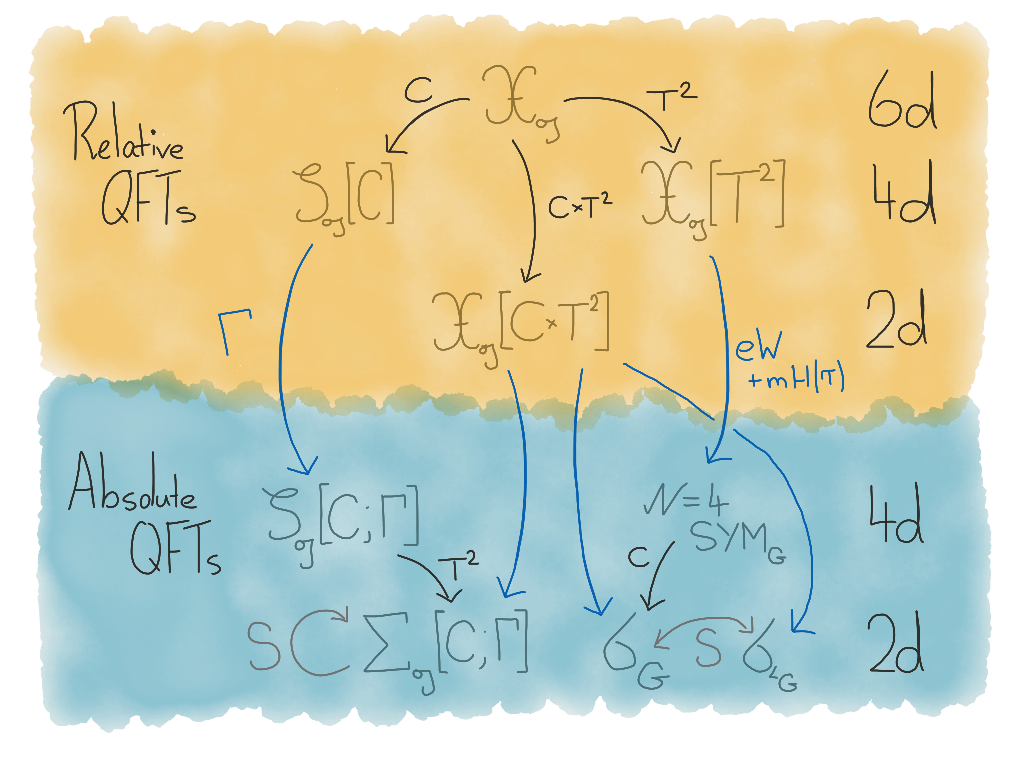
Certain symmetries of the higher dimensional theories are remembered by the lower dimensional theories. Following the right-hand path leads to SYM and the usual geometric Langlands duality, where the higher dimensional symmetry manifests as a symmetry exchanging two different 2d theories. Following the left-hand path leads to class \(\mathcal{S}\) and the self-dual geometric Langlands duality, where the higher dimensional symmetry manifests as a symmetry of a single theory. See (Derryberry, 2018) for details.
As part of this project, in (Derryberry, 2018; Derryberry, 2020) I extended the results of (Hausel & Thaddeus, 2003; Donagi & Pantev, 2012) to identify the SYZ mirror dual spaces for certain quotients of the moduli space of Higgs bundles, equipped with nontrivial B-fields. In examples where the input data for the moduli space is the same as the input data for a theory of class \(\mathcal{S}\) I observe that the moduli space is self dual, and I conjecture that it is the 3d Coulomb branch of the corresponding theory of class \(\mathcal{S}\). This is the content of the self-dual Dolbeault Langlands correspondence.
Future directions for this project include proving this conjecture, as well as extending to self-dual versions of the de Rham and quantum Langlands conjectures.
References:
- Electric-magnetic duality and the geometric Langlands programCommunications in Number Theory and Physics, 2007
- Wall-crossing, Hitchin systems, and the WKB approximationAdvances in Mathematics, 2013
- Fivebranes and knotsQuantum Topology, 2012
- Liouville correlation functions from four-dimensional gauge theoriesLetters in Mathematical Physics, 2010
- Relative quantum field theoryCommunications in Mathematical Physics, 2014
- Towards a Self-dual Geometric Langlands programPh.D. Thesis (University of Texas at Austin), 2018
- Stacky dualities for the moduli of Higgs bundlesAdvances in Mathematics, 2020
- Mirror symmetry, Langlands duality, and the Hitchin systemInventiones Mathematicae, 2003
- Langlands duality for Hitchin systemsInventiones Mathematicae, 2012